Pengertian dan Penjelasan tentnag Penarikan Kesimpulan,Aljabar Boolean, Gerbang Logika

TI_POLITALA_MATDIS_1A

Nama : Nordian

Kelas : 1A

Prodi : Tekinik Informatika

- PENARIKAN KESIMPULAN

Jika pernyataan atau proposisi dilambangkan dengan kalimat yang memiliki nilai benar saja atau salah saja, maka istilah sahih atau tidak sahih berkait dengan penarikan kesimpulan, penalaran, ataupun argumen. Beda kedua istilah menurut Soekardijo (1988) adalah, kalau penalaran itu aktivitas pikiran yang abstrak maka argumen ialah lambangnya yang berbentuk bahasa atau bentuk-bentuk lambang lainnya. Dikenal dua macam penarikan kesimpulan. Yang pertama adalah induksi atau penalaran induktif dan yang kedua adalah deduksi atau penalaran deduktif. Yang akan dibicarakan pada blog ini adalah penalaran deduktif atau deduksi. Contoh deduksi atau penalaran deduktif adalah:
Premis 1: Semua manusia akan mati.
Premis 2: Amri manusia.
Kesimpulan: Jadi, Amri pada suatu saat akan mati.

B. Sahih Tidaknya Penarikan Kesimpulan
Perhatikan contoh penarikan kesimpulan ini:
(1) Semarang terletak di sebelah barat Surabaya.
(2) Jakarta terletak di sebelah barat Semarang.
Jadi, Jakarta terletak di sebelah barat Surabaya.
Giere (1984) mencontohkan bahwa dari suatu premis-premis yang bernilai salah akan dapat dihasilkan suatu kesimpulan yang bernilai benar melalui suatu proses penarikan kesimpulan yang valid seperti:
Kuda adalah binatang bersayap.                                 (Salah)
Semua binatang bersayap tidak dapat terbang.         (Salah)
Jadi, kuda tidak dapat terbang                                   (Benar)
Giere (1984) mencontohkan juga bahwa dari suatu premis-premis yang bernilai salah akan dapat dihasilkan suatu kesimpulan yang bernilai salah melalui suatu contoh proses penarikan
kesimpulan yang valid berikut ini.
Bulan lebih besar daripada bumi.                                (Salah)
Bumi lebih besar daripada matahari.                           (Salah)
Jadi, bulan lebih besar daripada matahari                   (Salah)

c. Beberapa Penarikan Kesimpulan yang Sahih
Beberapa penarikan kesimpulan yang sahih atau valid yang akan dibahas pada bagian ini
di antaranya adalah modus ponens, modus tolens, dan silogisme.

Modus Ponens

Perhatikan contoh berikut.
Premis 1: Semua manusia akan mati
Premis 2: Amri manusia.
Kesimpulan: Jadi, Amri pada suatu saat akan mati.
Premis 1 adalah senilai dengan: Jika x manusia maka x akan mati. Pada contoh ini, premis-premis yang bernilai benar tidak akan memungkinkan bagi kesimpulannya untuk bernilai salah, sehingga penarikan kesimpulan bentuk seperti itu disebut dengan penarikan kesimpulan sah, sahih, valid, atau correct. Bentuk umumnya adalah:
p ⇒ q
p
∴ q
Untuk mengetahui validitas suatu argumen deduktif adalah dengan membentuk kondisional atau implikasi di mana konjungsi premis-premis dari argumen tersebut dijadikan   17sebagai antesedennya dan konklusi dari argumen tersebut dijadikan sebagai konsekuennya.
Sebagai contoh, untuk mengetahui valid tidaknya argumen berikut:
p ⇒ q   (Premis 1)
p          (Premis 2)
Jadi q (Kesimpulan)
adalah dengan membentuk konjungsi dari premis 1 dan 2, yaitu:
(p ⇒ q) ∧ p lalu konjungsi tersebut diimplikasikan dengan konklusi argumen yang ada sehingga menjadi: (p ⇒ q) ∧ p ⇒ q.
Bentuk terakhir ini harus dibuktikan melalui tabel kebenaran apakah termasuk tautologi atau tidak. Jika bentuk terakhir tadi merupakan tautologi maka argumen tadi valid. Jika tidak dihasilkan suatu tautologi maka argumen tadi tidak valid. Untuk membuktikannya, dapat ditunjukkan bahwa [(p ⇒ q) ∧ p] ⇒ q merupakan suatu tautologi lewat tabel kebenaran di bawah ini.

Pada langkah terakhir (langkah ke-4) terlihat nilai kebenarannya adalah semuanya benar (tautologi), sehingga modus ponens termasuk penarikan kesimpulan yang sah, valid, absah, atau sahih.
Contoh modus ponens:
a. Jika seseorang berada di Jakarta maka ia berada di Jawa.
Anita berada di Jakarta.
Jadi, Anita berada di pulau Jawa.
b. Pada hari Senin di sekolah ada pelajaran logika.
Tanggal 2 April 2001 adalah hari Senin.
Jadi, pada tanggal 2 April 2001 ada pelajaran logika.
c. Jika suatu segitiga mempunyai 2 sisi yang sama panjang maka segitiga itu sama kaki.
Pada segitiga ABC, AB = AC.
Jadi, segitiga ABC sama kaki.   18
2. Modus Tolens
Perhatikan contoh berikut.
Premis 1: Jika seseorang adalah siswa SMK maka ia pintar
Premis 2: Orang itu tidak pintar.
Kesimpulan: Orang itu bukan siswa SMK.
Pada contoh ini, premis-premis yang bernilai benar tidak memungkinkan bagi
kesimpulannya untuk bernilai salah juga, sehingga penarikan kesimpulan bentuk seperti itu disebut dengan penarikan kesimpulan sah, sahih, valid, atau correct. Bentuk umum modus tolens adalah:
p ⇒ q
~q
∴ ~p
Argumen di atas dapat dibuktikan sendiri seperti pada saat membuktikan modus ponens, yaitu dengan membuktikan implikasi [(p ⇒ q) ∧ (~ q)] ⇒ ~ p sebagai suatu tautologi.
Contoh modus tolens:
a. Seorang vegetarian tidak makan daging ataupun hasil olahannya.
Amin makan ayam goreng.
Jadi, Amin bukan vegetarian
b. Bilangan prima adalah bilangan yang faktornya adalah 1 dan dirinya sendiri
x mempunyai 3 buah faktor.
Jadi, x bukan bilangan prima.
c. Seluruh grafik y = ax² + bx + c terletak di atas sumbu-X bila     a > 0 dan b² – 4ac < 0
y = − 2x² + 4x – 5 dengan a = – 2 < 0
Jadi, tidak seluruh grafik y = − 2x² + 4x – 5 terletak di atas sumbu-X
3. Modus Silogisme
Perhatikan contoh ini.
(1) Rumah Amin terletak di sebelah barat rumah Akbar.
(2) Rumah Akbar terletak di sebelah barat rumah Abdur
Jadi, rumah Amin terletak di sebelah barat rumah Abdur
Tentunya para siswa dan Anda sendiri tidak akan mengetahui apakah ketiga orang tersebut benar-benar memiliki rumah seperti yang dinyatakan kalimat tersebut. Tetapi Anda dapat menyatakan bahwa jika premis-premisnya bernilai benar maka kesimpulannya tidaklah mungkin bernilai salah, sehingga penarikan kesimpulan seperti itu merupakan contoh penarikan kesimpulan yang sahih atau valid. Bentuk umum penarikan kesimpulan yang
dikenal dengan nama silogisme itu adalah:
p ⇒ q
q ⇒ r
∴p ⇒ r
Kesahihan argumen silogisme ini dapat dibuktikan sendiri seperti di atas, yaitu dengan menunjukkannya pada tabel kebenaran bahwa bentuk (p ⇒ q) ∧ (q ⇒ r) ⇒ (p ⇒ r)
Contoh Silogisme:
a. Setiap hari Sabtu ayah tidak bekerja (libur).
Ayah berkebun jika tidak bekerja.
Jadi, setiap hari Sabtu ayah berkebun.
b. Jika x dan y adalah dua bilangan bulat berurutan maka yang satu genap dan yang satunya lagi ganjil.
Jika salah satu bilangan genap dan yang satunya lagi ganjil maka jumlah kedua bilangan itu ganjil.
Jadi, jika x dan y bilangan bulat berurutan maka jumlah kedua bilangan itu ganjil.
Perlu diingatkan sekali lagi bahwa dalam penarikan kesimpulan, premis-premisnya diasumsikan atau dianggap benar dan argumennya harus valid, dan berikut ini adalah beberapa contoh soal tentang penarikan kesimpulan.
Contoh 1
Perhatikan premis-premis ini.
(1) Jika Anita mendapat A pada ujian akhir maka Anita mendapat A untuk mata kuliah itu.
(2) Jika Anita mendapat A untuk mata kuliah itu maka ia dinominasikan menerima beasiswa.
(3) Anita tidak dinominasikan menerima beasiswa.
Buatlah suatu kesimpulan dari tiga premis tersebut.
Penyelesaian
Misal        p: Anita mendapat nilai A pada ujian akhir
q: Anita mendapat nilai A untuk mata kuliah itu
r: Anita dinominasikan mendapat beasiswa
Peryataan-pernyataan di atas dapat diterjemahkan secara simbolik:
(1) p ⇒ q
(2) q ⇒ r
(3) ~ r
Dari premis (1) dan (2), dengan silogisme, akan diperoleh p ⇒ r. Jika dilanjutkan dengan premis (3) akan terjadi modus tolens berikut:
p ⇒ r
~r
∴ ~p
Kesimpulannya, Anita tidak mendapat nilai A pada ujian akhir.
Contoh 2:
Apakah penarikan kesimpulan berikut ini valid?
Jika x = 3 maka x²= 9
x²= 9
Jadi, x = 3
Penyelesaian:
Bentuk simbolik penarikan kesimpulan di atas adalah:
p ⇒ q
q
Jadi, p
Bentuk di atas bukan modus ponens, modus tolens, maupun silogisme. Untuk menentukan valid atau tidaknya, dibuat tabel kebenaran [(p ⇒ q)∧ q] ⇒ p berikut.

Nilai kebenaran [(p ⇒ q) ∧ p] ⇒ q yang diperlihatkan dalam langkah 4 ternyata bukan tautologi. Dengan demikian bentuk penarikan kesimpulan di atas tidak valid.
Argumen yang tidak valid lainnya berbentuk:
p ⇒ q
~p
~q

Modus Ponens

Modus ponens ditandai dengan adanya pernyataan majemuk implikasi dan pernyataan tunggal.

Modus Tollens

Modus tollens ditandai dengan adanya pernyataan majemuk implikasi dan ingkaran dari pernyataan tunggal.

Modus Silogisme

Modus silogisme ditandai dengan adanya dua pernyataan majemuk implikasi.

Masih belum paham bagaimana menarik kesimpulan dengan logika matematika? Latihan, yuk!

Premis 1: Jika semua harta benda Andi terbawa banjir, maka ia menderita.

Premis 2: Andi tidak menderita.

Kesimpulan yang sah dari premis-premis tersebut adalah…

Semua harta benda Andi tidak terbawa banjir.
Ada harta benda Andi yang terbawa banjir.
Semua harta benda Andi terbawa banjir.
Ada harta benda Andi yang tidak terbawa banjir.
Tidak ada banjir.

Pembahasan:

Dengan menggunakan modus tollen.

Premis 1: p => q

Premis 2: ~q

Konklusi: ~p

Jawaban: ~p = ada harta benda Andi yang tidak terbawa banjir (D).

- ALJABAR BOOLEAN

Dalam matematika dan ilmu komputer, Aljabar Boolean adalah struktur aljabar yang "mencakup intisari" operasi logika AND, OR, NOR, dan NAND dan juga teori himpunan untuk operasi union, interseksi dan komplemen.
Penamaan Aljabar Boolean sendiri berasal dari nama seorang matematikawan asal Inggris, bernama George Boole. Dialah yang pertama kali mendefinisikan istilah itu sebagai bagian dari sistem logika pada pertengahan abad ke-19.
Boolean adalah suatu tipe data yang hanya mempunyai dua nilai. Yaitu true atau false (benar atau salah).
Pada beberapa bahasa pemograman nilai true bisa digantikan 1 dan nilai false digantikan 0.

Pengertian Aljabar Boolean dan Hukumnya – Aljabar Boolean atau dalam bahasa Inggris disebut dengan Boolean Algebra adalah matematika yang digunakan untuk menganalisis dan menyederhanakan Gerbang Logika pada Rangkaian-rangkaian Digital Elektronika. Boolean pada dasarnya merupakan Tipe data yang hanya terdiri dari dua nilai yaitu “True” dan “False” atau “Tinggi” dan “Rendah” yang biasanya dilambangkan dengan angka “1” dan “0” pada Gerbang Logika ataupun bahasa pemrograman komputer. Aljabar Boolean ini pertama kali diperkenalkan oleh seorang Matematikawan yang berasal dari Inggris pada tahun 1854. Nama Boolean sendiri diambil dari nama penemunya yaitu George Boole.

Hukum Aljabar Boolean

Dengan menggunakan Hukum Aljabar Boolean ini, kita dapat mengurangi dan menyederhanakan Ekspresi Boolean yang kompleks sehingga dapat mengurangi jumlah Gerbang Logika yang diperlukan dalam sebuah rangkaian Digital Elektronika.

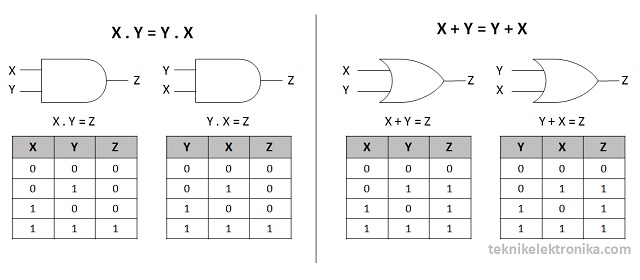
Hukum Komutatif (Commutative Law)

Hukum Komutatif menyatakan bahwa penukaran urutan variabel atau sinyal Input tidak akan berpengaruh terhadap Output Rangkaian Logika.
Contoh :
Perkalian (Gerbang Logika AND)
X.Y = Y.X
Penjumlahan (Gerbang Logika OR)
X+Y = Y+X
Catatan : Pada penjumlahan dan perkalian, kita dapat menukarkan posisi variabel atau dalam hal ini adalah sinyal Input, hasilnya akan tetap sama atau tidak akan mengubah keluarannya.

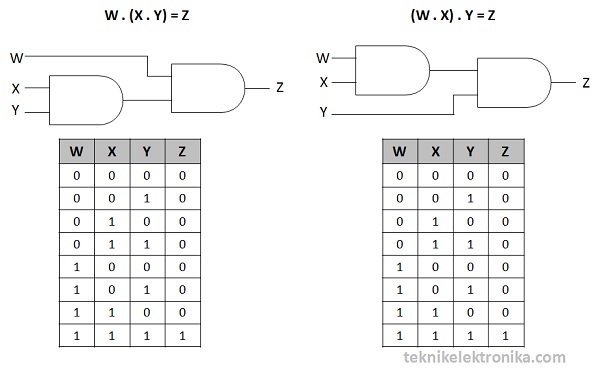
Hukum Asosiatif (Associative Law)

Hukum Asosiatif menyatakan bahwa urutan operasi logika tidak akan berpengaruh terhadap Output Rangkaian Logika.
Contoh :
Perkalian (Gerbang Logika AND)
W . (X . Y) = (W . X) . Y

Penjumlahan (Gerbang Logika OR)
W + (X + Y) = (W + X) + Y

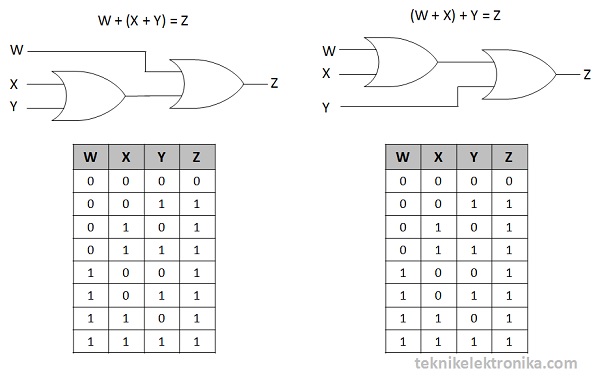
Catatan : Pada penjumlahan dan perkalian, kita dapat mengelompokan posisi variabel dalam hal ini adalah urutan operasi logikanya, hasilnya akan tetap sama atau tidak akan mengubah keluarannya. Tidak peduli yang mana dihitung terlebih dahulu, hasilnya tetap akan sama. Tanda kurung hanya sekedar untuk mempermudah mengingat yang mana akan dihitung terlebih dahulu.

Hukum Distributif

Hukum Distributif menyatakan bahwa variabel-variabel atau sinyal Input dapat disebarkan tempatnya atau diubah urutan sinyalnya, perubahan tersebut tidak akan mempengaruhi Output Keluarannya.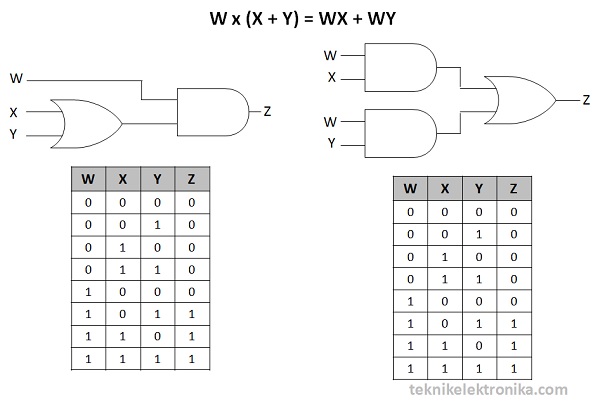

Hukum AND (AND Law)

Disebut dengan Hukum AND karena pada hukum ini menggunakan Operasi Logika AND atau perkalian. Berikut ini contohnya :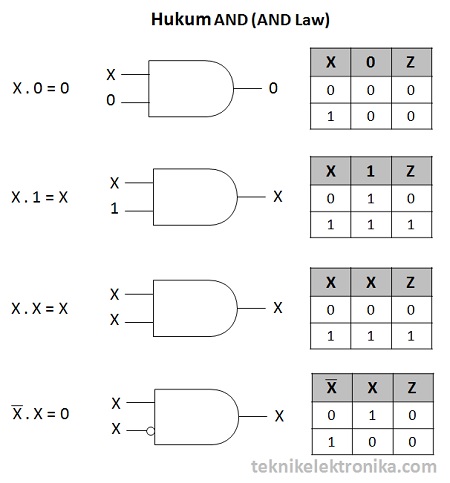

Hukum OR (OR Law)

Hukum OR menggunakn Operasi Logika OR atau Penjumlahan. Berikut ini adalah Contohnya :

Hukum Inversi (Inversion Law)

Hukum Inversi menggunakan Operasi Logika NOT. Hukum Inversi ini menyatakan jika terjadi Inversi ganda (kebalikan 2 kali) maka hasilnya akan kembali ke nilai aslinya.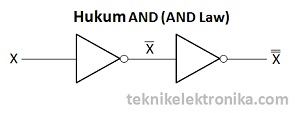

Jadi, jika suatu Input (masukan) diinversi (dibalik) maka hasilnya akan berlawanan. Namun jika diinversi sekali lagi, hasilnya akan kembali ke semula.

- GERBANG LOGIKA

Gerbang logika atau gerbang logik adalah suatu entitas dalam elektronika dan matematika Boolean yang mengubah satu atau beberapa masukan logik menjadi sebuah sinyal keluaran logik. Gerbang logika terutama diimplementasikan secara elektronis menggunakan diode atau transistor, akan tetapi dapat pula dibangun menggunakan susunan komponen-komponen yang memanfaatkan sifat-sifat elektromagnetik (relay), cairan, optik dan bahkan mekanik.

Gerbang Logika (Logic Gate) sebuah pemrosesan dasar yang berguna dalam memproses input-input berupa bilangan biner. Dengan kata lain gerbang logika beroperasi atau bekerja berdasarkan sistem bilangan biner, secara singkat sistem bilangan biner dapat diartikan sebagai jenis bilangan yang terdiri dari 2 kode angka yaitu "0" dan "1". Pastikan Anda memahami sistem bilangan biner terlebih dahulu sebelum mempelajari gerbang logika dasar lebih lanjut.

Fungsi dan Cara Kerja Gerbang Logika

Secara sederhana, fungsi dari gerbang logika adalah mengubah satu atau beberapa sinyal input (masukan) menjadi sebuah sinyal output (keluaran). Lalu bagaimana gerbang logika dapat mengubah sinyal input menjadi sinyal output logis ?

Untuk mengetahui hal tersebut, Anda wajib mengetahui jenis-jenis gerbang logika dasar. Terdapat sekitar 7 gerbang logika dasar yang berguna dalam membentuk sebuah rangkaian sistem elektronika digital.

1. Gerbang Logika NOT
2. Gerbang Logika AND
3. Gerbang Logika OR
4. Gerbang Logika NAND
5. Gerbang Logika NOR
6. Gerbang Logika X-OR
7. Gerbang Logika X-NOR

Dari setiap jenis gerbang logika dasar diatas memiliki tabel kebenaran yang berbeda, dimana fungsi dari tabel kebenaran gerbang logika yaitu sebagai acuan dalam penentuan sinyal output dari sebuah rangkaian gerbang logika. Dengan kata lain, untuk mengetahui bagaimana sebuah gerbang logika bekerja maka diharuskan untuk mengetahui tabel kebenaran dari setiap gerbang logika.

Tabel kebenaran gerbang logika tersebut berisikan kombinasi variabel input (masukan) sehingga akan menghasilkan variabel output (keluaran) logis.

Adapun variabel input dan output pada gerbang logika hanya memiliki 2 keadaan. 2 keadaan (level) ini dapat dilambangkan sebagai berikut

1 dan 0
HIGH (Tinggi) dan LOW (Rendah)
TRUE (Benar) dan False (Salah)
ON (Hidup) dan Off (Mati)

Salah satu contoh sederhana dalam penerapan gerbang logika dalam rangkaian elektronika adalah dengan menggunakan Transistor TTL, bila keadaan 0 V pada rangkaian diasumsikan sebagai "LOW" maka keadaan 5 V pada rangkaian diasumsikan sebagai "HIGH"

7 Jenis Gerbang Logika

Berikut ini kami sajikan 7 jenis gerbang logika dasar yang paling umum dipergunakan, disertai pula dengan simbol dan tabel kebenarannya.

Gerbang AND (AND GATE)

Gerbang AND atau disebut juga "AND GATE" adalah jenis gerbang logika yang memiliki dua input (Masukan) dan satu output (keluaran). Untuk lebih jelasnya perhatikan simbol dan tabel kebenaran gerbang AND berikut.

Pada gerbang logika AND, simbol yang menandakan operasi gerbang logika AND adalah tanda titik (.) atau bisa juga dengan tanpa tanda titik, contohnya seperti Z = X.Y atau Z = XY.

Perhatikan tabel kebenaran gerbang AND. Cara cepat untuk mengingat tabelnya adalah dengan mengingat pernyataan berikut. "Gerbang AND akan menghasilkan output (keluaran) logika 1 bila semua variabel input (masukan) bernilai logika 1" sebalikanya "Gerbang AND akan menghasilkan keluaran logika 0 bila salah satu masukannya merupakan logika 0". Cukup mudah bukan..

Gerbang OR (OR GATE)

Gerbang OR atau disebut juga "OR GATE" adalah jenis gerbang logika yang memiliki dua input (Masukan) dan satu output (keluaran). Meskipun memiliki pengertian yang sama dengan gerbang OR tapi memiliki perbedaan pada simbol dan tabel kebenaran. Untuk lebih jelasnya perhatikan simbol dan tabel kebenaran gerbang OR berikut.

Pada gerbang logika AND, simbol yang menandakan operasi gerbang logika AND adalah tanda tambah (+) , contohnya seperti Z = X + Y .

Perhatikan tabel kebenaran gerbang OR. Cara cepat untuk mengingat tabelnya adalah dengan mengingat pernyataan berikut. "Gerbang AND akan menghasilkan output (keluaran) logika 0 bila semua variabel input (masukan) bernilai logika 0" sebalikanya "Gerbang AND akan menghasilkan keluaran logika 1 bila salah satu masukannya bernilai logika 1". Jangan sampai terbalik dengan pernyataan Gerbang AND.

Gerbang NOT (NOT GATE)

Gerbang NOT atau disebut juga "NOT GATE" atau Inverter (Gerbang Pembalik) adalah jenis gerbang logika yang hanya memiliki satu input (Masukan) dan satu output (keluaran). Dikatakan Inverter (gerbang pembalik) karena gerbang ini akan menghasilkan nilai ouput yang berlawanan dengan nilai inputnya . Untuk lebih jelasnya perhatikan simbol dan tabel kebenaran gerbang NOT berikut.

Pada gerbang logika NOT, simbol yang menandakan operasi gerbang logika NOT adalah tanda minus (-) diatas variabel, perhatikan gambar diatas.

Perhatikan tabel kebenaran gerbang NOT. Cara cepat untuk mengingat tabelnya adalah dengan mengingat pernyataan berikut. "Gerbang NOT akan menghasilkan output (keluaran) logika 1 bila variabel input (masukan) bernilai logika 0" sebalikanya "Gerbang NOT akan menghasilkan keluaran logika 0 bila input (masukan) bernilai logika 1".

Gerbang NAND (NAND GATE)

Gerbang NAND atau disebut juga "NAND GATE" adalah jenis gerbang logika kombinasi yang memiliki dua input (Masukan) dan satu output (keluaran). Pada dasarnya gerbang NAND merupakan pengembangan atau kombinasi dari gerbang AND dan gerbang NOT "NAND = NOT AND". Untuk lebih jelasnya perhatikan simbol dan gerbang kebenaran gerbang NAND berikut.

Pada gerbang logika NAND, simbol yang menandakan operasi gerbang logika NAND adalah tanda bar (-) diatas variabel, perhatikan gambar diatas.

Perhatikan tabel kebenaran gerbang NAND. Cara cepat untuk mengingat tabelnya adalah dengan mengingat pernyataan berikut. "Gerbang NAND akan menghasilkan output logika 0 bila semua inputnya memiliki logika 1" sedangkan " Gerbang NAND akan menghasilkan keluaran logika 1 bila salah satu input atau semua input memiliki logika 0".

Secara singkat, cukup mengingat gerbang logika AND, karena output dari gerbang logika NAND merupakan kebalikan dari output gerbang AND.

Gerbang NOR (NOR GATE)

Gerbang NOR atau "NOR GATE" merupakan pengembangan dari gabungan kombinasi gerbang OR dan gerbang NOT. Gerbang ini juga memiliki dua input dan 1 satu keluaran, untuk lebih jelasnya perhatikan gambar simbol dan tabel kebenaran dibawah.

Pada gerbang logika NOR, simbol yang menandakan operasi gerbang logika NAND adalah tanda tanbah (+) dan bar (-) diatas variabel, perhatikan gambar diatas.

Perhatikan tabel kebenaran gerbang NOR. Cara cepat untuk mengingat tabelnya adalah dengan mengingat pernyataan berikut. "Gerbang NOR akan menghasilkan output logika 1 bila semua inputnya memiliki logika 0" sedangkan " Gerbang NOR akan menghasilkan keluaran logika 0 bila salah satu input atau semua input memiliki logika 1".

Secara singkat, sama halnya dengan gerbang AND. Output gerbang NOR merupakan kebalikan ouput gerbang OR, jadi cukup mengingat gerbang OR saja lalu membaliknya.

Gerbang X-OR (X-OR GATE)

Gerbang Exclusive OR atau disingkat gerbang X-OR, terdiri dari 2 input dan 1 output. Untuk lebih jelasnya perhatikan gambar simbol dan tabel kebenaran dibawah.

Untuk mengingat tabel kebenaran gerbang X-OR cukup mengingat pernyataan berikut ini. "Bila kedua input bernilai logika yang sama maka akan menghasilkan output logika 0" sedangkan "Bila kedua input bernilai logika berbeda maka akan menhasilkan output logika 1".

Gerbang X-NOR (X-NOR GATE)

Gerbang X-NOR merupakan kombinasi dari gerbang X-OR dan gerbang NOT. Perhatikan simbol dan tabel kebenaran gerbang X-NOR berikut.

Karena merupakan kebalikan dari gerbang X-OR, maka untuk mengingat tabel kebenaran gerbang logika X-NOR untuk dengan mengingat tabel kebenaran gerbang logika X-OR lalu membalik nilai outputnya.

Penerapan Gerbang Logika

Gerbang logika kebanyakan dipergunakan dalam sistem elektronika digital dengan menggunakan komponen-komponen elektronika seperti integrated circuit (IC), transistor, relay, dioda, optik maupun elemen mekanikal.

- SUMBER :

https://smartblogmathematic.wordpress.com/penarikan-kesimpulan/
https://blog.ruangguru.com/belajar-menarik-kesimpulan-dengan-logika-matematika

http://webstudi.blogspot.com/2017/05/gerbang-logika.html

https://id.wikipedia.org/wiki/Gerbang_logika

https://teknikelektronika.com/pengertian-aljabar-boolean-hukum-aljabar-boolean/

https://id.wikipedia.org/wiki/Aljabar_Boolean