
1. PENGERTIAN TREE
Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang
membentuk layakya struktur sebuah pohon. Struktur pohon adalah suatu cara
merepresentasikan suatu struktur hirarki (one-to-many) secara grafis yang mirip
sebuah pohon, walaupun pohon tersebut hanya tampak sebagai kumpulan node-node dari atas ke bawah. Suatu struktur data yang tidak linier yang
menggambarkan hubungan yang hirarkis (one-to-many) dan tidak linier antara
elemen-elemennya.
Deklarasi Pohon
Jika kita memperhatikan setiap simpul dalam pohon biner, kita bisa menyusun struktur data yang tepat dari simpul-simpul tersebut. Kita dapat melihat bahwa dalam setiap simpul selalu berisi dua buah pointer untuk menunjuk ke cabang kiri dan cabang kanan, dan informasi yang akan disimpan dalamsimpul tersebut. Dengan memperhatikan hal ini, simpul dalam pohon biner disajikan sebagai berikut:
Sesuai dengan gambar 7.1, maka deklarasi list yang sesuai adalah:
typedef char TypeInfo;
typedef struct Simpul *Tree;
struct Simpul {
TypeInfo Info;
tree Kiri, /* cabang kiri */
Kanan; /* cabang kanan */
};
ISTILAH DALAM TREE
- JENIS-JENIS TREE
BINARY TREE
Tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal dua sub
pohon dan kedua subpohon harus terpisah.
Kelebihan struktur Binary Tree :
- Mudah dalam penyusunan algoritma sorting
- Searching data relatif cepat
- Fleksibel dalam penambahan dan penghapusan data
- KUNJUNGAN PADA POHON BINER
Sebuah pohon biner memiliki operasi traversal yaitu suatu kunjungan pada
suatu simpul tepat satu kali. Dengan melakukan kunjungan lengkap kita akan
memperoleh urutan informasi secara linier yang tersinpan di dalam pohon biner.
Terdapat tiga jenis kunjungan pada pohon biner, yaitu :
- PREORDER
Kunjungan jenis ini mempunyai urutan kunjungan sebagai berikut :
– Cetak isi simpul yang dikunjungi.
– Kunjungi cabang kiri.
– Kunjungi cabang kanan.
Prosedur untuk melakukan traversal secara PREORDER adalah sebagai berikut:
- INORDER
Kunjungan jenis ini mempunyai urutan kunjungan sebagai berikut :
– Kunjungi cabang kiri.
– Cetak isi simpul yang dikunjungi.
– Kunjungi cabang kanan.
Prosedur untuk melakukan traversal secara INORDER adalah sebagai berikut:
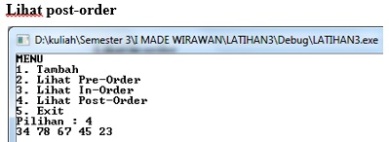
- POSTORDER
Kunjungan jenis ini mempunyai urutan kunjungan sebagai berikut :
– Kunjungi cabang kiri.
– Kunjungi cabang kanan.
– Cetak isi simpul yang dikunjungi
BERIKUT MERUPAKN CONTOH PROGRAMNYA
#include<stdio.h>//header file
#include<conio.h>
/* Deklarasi struct */
typedef struct Node{
int data; //data pada tree
Node *kiri; //penunjuk node anak kiri
Node *kanan; //penunjuk node anak kanan
};
/* Fungsi untuk memasukkan data ke dalam tree */
void tambah(Node **root, int databaru){
if((*root) == NULL){ //jika pohon/subpohon masih kosong
Node *baru;//node “baru” dibentuk…
baru = new Node;//berdasarkan struct “Node”
baru->data = databaru; //data node baru diisi oleh variabel databaru
baru->kiri = NULL;//penunjuk kiri node baru masih kosong
baru->kanan = NULL;//penunjuk kanan node baru masih kosong
(*root) = baru; //node pohon (root) diletakkan pada node baru
(*root)->kiri = NULL;//penunjuk kiri node root masih kosong
(*root)->kanan = NULL; //penunjuk kanan node root masih kosong
printf(“Data bertambah!”);
}
else if(databaru < (*root)->data)//jika databaru kurang dari data node root…
tambah(&(*root)->kiri, databaru);//tambahkan databaru pada subpohon kiri
else if(databaru > (*root)->data)//jika databaru lebih dari data node root…
tambah(&(*root)->kanan, databaru); //tambahkan databaru pada subpohon kanan
else if(databaru == (*root)->data)//jika databaru sama dengan data node root
printf(“Data sudah ada!”);//databaru tidak dapat ditambahkan pada tree
}
/* Fungsi untuk menampilkan data secara pre-order
(data ditampilkan dari node induk, node anak kiri, lalu node anak kanan)
*/
void preOrder(Node *root){
if(root != NULL){//jika pohon/subpohon tidak kosong
printf(“%d “, root->data);//menampilkan data node yang dikunjungi
preOrder(root->kiri);//mengunjungi node anak kiri
preOrder(root->kanan); //mengunjungi node anak kanan
}
}
/* Fungsi untuk menampilkan data secara in-order
(data ditampilkan dari node anak kiri, node induk, lalu node anak kanan)
*/
void inOrder(Node *root){
if(root != NULL){//jika pohon/subpohon tidak kosong…
inOrder(root->kiri);//mengunjungi node anak kiri
printf(“%d “, root->data);//menampilkan data node yang dikunjungi
inOrder(root->kanan);//mengunjungi node anak kanan
}
}
/* Fungsi untuk menampilkan data secara post-order
(data ditampilkan dari node anak kiri, node anak kanan, lalu node induk)
*/
void postOrder(Node *root){
if(root != NULL){//jika pohon/subpohon tidak kosong
postOrder(root->kiri); //mengunjungi node anak kiri
postOrder(root->kanan);//mengunjungi node anak kanan
printf(“%d “, root->data); //menampilkan data node yang dikunjungi
}
}
main(){
int pil, c;
Node *pohon, *t;
pohon = NULL;
do{
int data;
printf(“MENU\n”);
printf(“1. Tambah\n”);
printf(“2. Lihat Pre-Order\n”);
printf(“3. Lihat In-Order\n”);
printf(“4. Lihat Post-Order\n”);
printf(“5. Exit\n”);
printf(“Pilihan : “); scanf(“%d”, &pil);
switch(pil){
case 1 :
printf(“Data baru : “);
scanf(“%d”, &data);
tambah(&pohon, data);
break;
case 2 :
if(pohon != NULL)
preOrder(pohon);
else
printf(“Masih kosong!”);
break;
case 3 :
if(pohon != NULL)
inOrder(pohon);
else
printf(“Masih kosong!”);
break;
case 4 :
if(pohon != NULL)
postOrder(pohon);
else
printf(“Masih kosong!”);
break;
}
getch();
printf(“\n”);
}
while(pil != 5);
}
HASIL

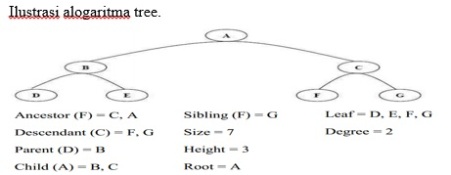
Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus yang disebut Root dan node lainnya terbagi menjadi himpunan-himpunan yang saling tak berhubungan satu sama lainnya (disebut subtree). Untuk jelasnya, di bawah akan diuraikan istilah-istilah umum dalam tree :
a) Prodecessor : node yang berada diatas node tertentu.
b) Successor : node yang berada di bawah node tertentu.
c) Ancestor : seluruh node yang terletak sebelum node tertentu dan terletak pada jalur yang sama.
d) Descendant : seluruh node yang terletak sesudah node tertentu dan terletak pada jalur yang sama.
e) Parent : predecssor satu level di atas suatu node.
f) Child : successor satu level di bawah suatu node.
g) Sibling : node-node yang memiliki parent yang sama dengan suatu node.
h) Subtree : bagian dari tree yang berupa suatu node beserta descendantnya dan memiliki semua karakteristik dari tree tersebut.
i) Size : banyaknya node dalam suatu tree.
j) Height : banyaknya tingkatan/level dalam suatu tree.
k) Root : satu-satunya node khusus dalam tree yang tak punya predecssor.
l) Leaf : node-node dalam tree yang tak memiliki seccessor.
m) Degree : banyaknya child yang dimiliki suatu node.
Beberapa jenis Tree yang memiliki sifat khusus :
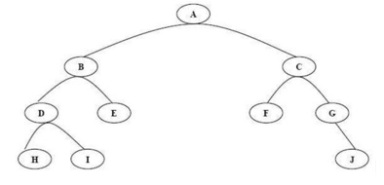
1) Binary Tree
Binary Tree adalah tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal dua subtree dan kedua subtree tersebut harus terpisah. Sesuai dengan definisi tersebut, maka tiap node dalam binary tree hanya boleh memiliki paling banyak dua child.
Jenis-jenis Binary Tree :
a) Full Binary Tree
 Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
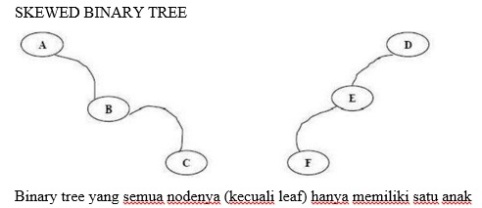
Mirip dengan Full Binary Tree, namun tiap subtree boleh memiliki panjang path yang berbeda. Node kecuali leaf memiliki 0 atau 2 child.
c) Skewed Binary Tree
Implementasi Binary Tree
Binary Tree dapat diimplemntasikan dalam Pascal dengan menggunakan double Linked List. Untuk nodenya, bisa dideklarasikan sbb :
Type Tree = ^node;
Node = record
Isi : TipeData;
Left,Right : Tree;
end;
Contoh ilustrasi Tree yang disusun dengan double linked list :
(Ket: LC=Left Child; RC=Right Child)
Operasi-operasi pada Binary Tree :
v Create : Membentuk binary tree baru yang masih kosong.
v Clear : Mengosongkan binary tree yang sudah ada.
v Empty : Function untuk memeriksa apakah binary tree masih kosong.
v Insert : Memasukkan sebuah node ke dalam tree. Ada tiga pilihan insert: sebagai root, left child, atau right child. Khusus insert sebagai root, tree harus dalam keadaan kosong.
v Find : Mencari root, parent, left child, atau right child dari suatu node. (Tree tak boleh kosong)
v Update : Mengubah isi dari node yang ditunjuk oleh pointer current. (Tree tidak boleh kosong)
v Retrieve : Mengetahui isi dari node yang ditunjuk pointer current. (Tree tidak boleh kosong)
v DeleteSub : Menghapus sebuah subtree (node beserta seluruh descendantnya) yang ditunjuk current. Tree tak boleh kosong. Setelah itu pointer current akan berpindah ke parent dari node yang dihapus.
v Characteristic : Mengetahui karakteristik dari suatu tree, yakni : size, height, serta average lengthnya. Tree tidak boleh kosong. (Average Length = [jumlahNodeLvl1*1+jmlNodeLvl2*2+…+jmlNodeLvln*n]/Size)
v Traverse : Mengunjungi seluruh node-node pada tree, masing-masing sekali. Hasilnya adalah urutan informasi secara linier yang tersimpan dalam tree. Ada tiga cara traverse : Pre Order, In Order, dan Post Order.
Langkah-Langkahnya Traverse :
Ø PreOrder : Cetak isi node yang dikunjungi, kunjungi Left Child, kunjungi Right Child.
Ø InOrder : Kunjungi Left Child, Cetak isi node yang dikunjungi, kunjungi Right Child.
Ø PostOrder : Kunjungi Left Child, Kunjungi Right Child, cetak isi node yang dikunjungi.
Untuk lebih jelasnya perhatikan contoh operasi-operasi pada Binary Tree berikut ini :
2) Binary search Tree
Adalah Binary Tree dengan sifat bahwa semua left child harus lebih kecil daripada right child dan parentnya. Juga semua right child harus lebih besar dari left child serta parentnya. Binary seach tree dibuat untuk mengatasi kelemahan pada binary tree biasa, yaitu kesulitan dalam searching / pencarian node tertentu dalam binary tree. Contoh binary search tree umum :
Pada dasarnya operasi dalam binary search tree sama dengan Binary tree biasa, kecuali pada operasi insert, update, dan delete.
1. Insert : Pada Binary Search Tree, insert dilakukan setelah ditemukan lokasi yang tepat. (Lokasi tidak ditentukan oleh user sendiri).
2. Update : Seperti pada Binary Tree biasa, namun disini uapte akan berpengaruh pada posisi node tersebut selanjutnya. Bila setelah diupdate mengakibatkan tree tersebut bukan Binary Search Tree lagi, maka harus dilakukan perubahan pada tree dengan melakukan perubahan pada tree dengan melakukan rotasi supaya tetap menjadi Binary Search Tree.
3. Delete : Seperti halnya update, delete dalam Binary Search Tree juga turut mempengaruhi struktur dari tree tersebut.
(Keadaan awal merupakan lanjutan gambar sebelumnya)
Pada operasi di samping, delete dilakukan terhadap Node dengan 2 child. Maka untuk menggantikannya, diambil node paling kiri dari Right SubTree yaitu 13.
2. GRAP
Graph adalah sekumpulan noktah (simpul/vertex) di dalam bidang dua dimensi yang dihubungkan dengan sekumpulan garis (sisi/edge). Graph dapat digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Sedangkan Pohon (tree) adalah graph yang khusus. Pohon dapat didefinisikan sebagai graph-tak-berarah terhubung yang tidak mengandung sirkuit (cycle).
Perbedaan antara graph dengan tree yaitu pada graph, mampu terjadi cycle, artinya dari suatu titik yang terhubung oleh edge dapat kembali lagi ke vertex tersebut. Sedangkan tree, merupakan suatu graf yang alur edge nya tidak dapat kembali lagi ke vertex awalnya.
Sebuah graf dibentuk dari kumpulan titik yang dihubungkan dengan garis – garis.
Ada beberapa istilah yang berhubungan dengan graph, antara lain :
- a. Titik – titik tersebut disebut vertex.
- b. Garis – garis yang menghubungkan antar vertex disebut edge.
- Adjacent artinya bertetangga. Maksudnya jika ada dua vertex disebut adjacent, jika mempunyai edge yang sama.
- Weight adalah bobot yang biasanya terdapat pada edge yang merepresentasikan jarak dari vertex-vertex yang dihubungkan oleh edgetersebut.
- Path adalah lintasan yang melalui edge dan vertex dalam graf.
- Cycle adalah lintasan yang dimulai dan berakhir pada vertex yang sama. Cyclekadang – kadang disebut circuit.
- Direct pada directed graph adalah graf dimana edge-edgenya mempunyai suatu arah.
Macam – macam representasi graph dalam struktur data:
· Dengan Array
yaitu pada suatu graf, hubungan antar simpul/vertexnya direpresentasikan dengan array dua dimensi, misalnya Array[m][n], dimana m dan n merupakan kolom dan baris yang merepresentasikan simpul-simpulnya dan nilai dari array tersebut menandakan hubungan antar simpul. Apakah terdapat sisi yang menghubungkan kedua simpul tersebut atau tidak.
Contoh Graf
Array yang terbentuk :
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 |
| 2 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 1 | 1 |
| 5 | 1 | 1 | 0 | 1 | 0 | 0 |
| 6 | 0 | 0 | 0 | 1 | 0 | 0 |
Contohnya:
Pada kolom ke 1 baris 1 bernilai 1 menandakan simpul 1 dengan simpul 1 itu sendiri saling terhubung. Begitu juga dengan kolom ke 2 baris 1 dan sebaliknya baris ke 2 kolom 1 bernilai 1 juga menandakan adanya hubungan antara simpul 2 dengan simpul 1.
Sedangkan nilai 0 menandakan bahwa antara kedua simpul tersebut tidak saling berhubungan.
· Dengan Linked List yaitu node/vertex dari graf tersebut direpresentasikan dengan linked list dari header node. Setiap dari header node tersebut berisi dua sampai tiga field atau lebih sesuai dengan kebutuhan. Pada graf berarah dan tak berbobot (directed-unweighted graph) minimal dibutuhka tiga field yaitu: info, nextVtx, edgePtr. info berisi informasi tentang vertex tersebut seperti nama vertex atau semacamnya, nextVtx adalah pointer yang menunjuk ke vertex selanjutnya jika ada. Sedangkan edgePtr adalah pointer yang menunjuk ke edge dari vertex tersebut. Ilustrasi Node untuk Vertex dan Edge dengan Linked List Contoh Graf Berarah-Tak Berbobot Ilustrasi Linked List dalam Graf Representasi graph terbaik menurut kami yaitu dengan menggunakan linked list. Merepresentasikan graph dengan matriks adjacency seperti pada array tidak mencukupi karena membutuhkan info lebih lanjut mengenai jumlah node. Jika sebuah graph harus dibentuk dalam rangka pemecahan masalah, atau harus diperbarui secara dinamik selama program berlangsung, sebuah matriks baru harus dibuat pada setiap penambahan atau penghapusan suatu node sehingga tidak efisien, khususnya dalam dunia nyata dimana suatu graph bisa memiliki ratusan atau lebih node. Jadi akan lebih baik jika membuat graph menggunakan linked list.
1. Shortest Path Problem adalah problem bagaimana kita mencari sebuah jalur pada graf yang meminimalkan jumlah bobot sisi pembentuk jalur tersebut.
Macam- macam algoritmanya :
a. Algoritma Dijkstra adalah sebuah greedy algorithm dalam memecahkan permasalahan jarak terpendek (shortest path problem) untuk sebuah simple graph takberarah (undirected graph) dengan bobot-bobot sisi (edge weights) yang bernilai tak-negatif. Algoritma Djikstra bekerja dengan cara mengunjungi simpul-simpul pada graf dimulai dengan simpul sumber. Kemudian secara berulang memilih simpul-simpul terdekat dan menghitung total bobot semua sisi yang dilewati untuk mencapai simpul tersebut. ·
Menandai simpul awal dengan [0,-] dan statusnya permanen · Beri label untuk node yang dapat berhubungan dengan node permanen dengan [a,b] dan status temporary dimana: a = jarak terpendek ke node awal b = node sebelumnya/yang mendahului ·
Mencari a terkecil dan status temporary berubah menjadi permanen · Apabila status sudah permanen semua maka proses berhenti, tetapi apabila belum akan kembali ke langkah b.
b. Algoritma Bellman-Ford adalah salah satu algoritma dalam penyelesaian shortest path problem untuk weighted-directed graph (graf berarah) dimana jika ada salah satu edge-nya yang bernilai negatif. Jika dalam graf tersebut terdapat suatu cycle, dari edge negatif maka algoritma Bellman-Ford hanya bisa mendeteksinya, dan algoritma ini tidak dapat menemukan shortest path yang tidak mengulangi beberapa vertex dari graf semacam itu.
Menentukan vertex source dan daftar seluruh vertices maupun edges · Assign nilai untuk distance dari vertex source = 0, dan yang lain infinite ·
Mulailah iterasi terhadap semua vertices yang dimulai dari vertex source, untuk menentukan distance dari semua vertices yang berhubungan dengan vertex source dengan formula seperti berikut ini :
– U = vertex asal
– V = vertex tujuan
– UV = Edges yang menghubungkan U dan V
– Jika distance V, lebih kecil dari distance U + weight UV maka distance V, diisi dengan distance U + weight UV
– Lakukan hingga semua vertices terjelajahi.
Untuk mengecek apakah ada negative cycle dalam graf tersebut lakukan iterasi untuk semua edges yang ada, kemudian lakukan pengecekan seperti dibawah ini: Untuk semua edges UV, jika ada distance vertex U + weight edges UV kurang dari distance vertex V maka sudah jelas bahwa graf tersebut memiliki negative cycle.
c. Algoritma Floyd merupakan algoritma untuk pencarian lintasan terpendek pada suatu graf berbobot (weighted graph). Algoritma Floyd-Warshall membandingkan semua kemungkinan lintasan pada graf untuk setiap sisi dari semua simpul. Cara kerja algoritma Floyd adalah sebagai berikut:
· Representasikan graf dengan N buah simpul dan bobotnya dengan menggunakan dua buah matriks ketetanggaan, matriks M untuk bobot dan Matriks Z untuk lintasan.
· Manipulasi keduanya sebanyak N iterasi.
· Matriks M hasil manipulasi akan menghasilkan bobot akhir
· Telusuri Matriks Z untuk mendapatkan lintasan terpendek
d. Algoritma Johnson adalah algoritma yang digunakan untuk mencari jarak terdekat, dimana di dalamnya juga terdapat algoritma Bellman Ford dan algoritma Dijkstra dalam menentukan nilai-nilainya
· Langkah awal penyelesaian Algoritma Johnson adalah mengkonstruksi digraph baru dengan menambahkan titik baru pada digraph dan memberi bobot sisi yang keluar dari titik baru tersebut dengan 0.
· Langkah selanjutnya adalah mencari lintasan terpendek dari titik baru ke semua titik lain. Lintasan terpendek tersebut digunakan untuk mengubah bobot semua sisi pada digraph baru agar bobot semua sisi bernilai positif.
· Setelah itu mencari lintasan terpendek dari tiap titik ke semua titik lain dan mengubah hasilnya dengan menggunakan lintasan terpendek dari titik baru ke semua titik lain.
· Hasil dari perhitungan ini berupa matriks. Dari matriks ini dapat diketahui panjang lintasan terpendek dari tiap titik ke semua titik lain.
a. Travelling Salesman Problem (TSP)
adalah suatu permasalahan dimana seorang salesman harus mengunjungi semua kota dimana tiap kota hanya dikunjunjungi sekali, dan dia harus mulai dari dan kembali ke kota asal. Tujuannya adalah menentukan rute dengan jarak total atau biaya paling minimum
Salah satu algoritma yang dapat dipakai yaitu algoritma Heuristik yang mencari nilai minimum bobot dengan menggunakan spanning tree sehingga menghasilkan irisan dari graf yang memiliki nilai optimal. Proses selanjutnya adalah membentuk sirkuit Euler. Lalu simpul yang dilalui lebih dari satu kali diperbaiki sehingga menghasilkan solusi paling optimal.
Langkah-langkahnya adalah sebagai berikut:
- Cari minimum spanning tree yang menghubungkan tiap n simpul dari graph yang kita namakan dengan network A
- Tentukan simpul graph berderajat, jika k jumlah simpul berderajat ganjil, maka k pasti genap. Kita pasangkan k simpul sehingga panjang cabang yang menghubungkan simpul minimum. Pasangan simpul yang mempunyai nilai minimum membentuk jaringan yang dinamakan network B. Network A dan B digabung menjadi network C.
- jaringan C tidak mempunyai simpul berderajat ganjil. Kita dapat menggambarkan sirkuit Euler di network C. Network C merupakan aproksimasi solusi dari travelling salesman problem.
- Periksa setiap simpul pada network C yang dikunjungi lebih dari satu kali dan perbaiki solusi travelling salesman problem, dengan menerapkan ketidaksamaan 1(a,b) < 1(a,c) + 1(b,c)
b. Chinese Postman Problem (CPP)
Masalah Chinese Postman Problem pertama kali diformulasikan dalam bentuk masalah untuk menentukan sisi terpendek bagi seorang tukang pos untuk melewati semua jalan yang ada dan kembali ke tempat semula. Masalah ini dikemukakan oleh Kwan Mei-Ko di awal 1960-an dalam jurnal Chinese Mathematics. Dalam istilah graf definisi CPP adalah mencari lintasan pada suatu graf berbobot yang terhubung yang melewati semua sisi (minimal sekali) dengan jumlah bobot minimum dari suatu simpul kembali ke simpul awal. Masalah ini dapat terjadi pada graf berarah, tidak berarah, dan graf campuran. Solusi untuk graf tidak berarah dan berarah dapat diselesaikan secara efisien dalam waktu polinomial, sedangkan solusi untuk graf campuran ternyata sulit didapat (termasuk dalam kategori masalah NP-Complete). Dasar untuk menyelesaikan masalah CPP adalah keberadaan sirkuit dan lintasan Euler.
Algoritmanya adalah :
· Jika graf adalah graf genap, maka hanya menentukan jalur Euler graf.
· Jika graf ganjil, maka:
- Menghitung dan kumpulkan simpul-simpul yang berderajat ganjil.
- Mencari jalur-jalur terpendek yang menghubungkan simpul-simpul ganjil.
- Menggandakan jalur-jalur tersebut secara virtual yaitu dengan melewat sisi dua kali
c. Coloring Graph
atau pewarnaan graf adalah pemberian warna terhadap vertex-vertex graf dimana dua buah vertex yang berdampingan tidak boleh mempunyai warna yang sama. G bewarna n artinya graf tersebut menggunakan n warna. Bilangan kromatis dari G = K(G) adalah jumlah minimum warna yang dibutuhkan.
Algoritma yang dapat digunakan untuk menyelesaikan permasalahan pewarnaan graf salah satunya adalah algoritma Greedy. Langkah-langkahnya sebagai berikut:
· Inisialisasi himpunan solusi dengan kosong.
· Urutkan vertex berdasarkan jumlah edge terbanyak.
· Melakukan pemilihan vertex yang akan diisi warnanya dengan fungsi seleksi vertex.
· Memilih kandidat warna dengan menggunakan kandidat kurangi warna anggota himpunan kandidat dengan warna yang diambil.
· Periksa kelayakan warna yang dipilih menggunakan langkah ketiga. Jika layak dimasukkan ke himpunan solusi.
· Periksa apakah solusi sudah meliputi pewarnaan seluruh vertex. Jika sudah maka berhenti, jika belum maka akan kembali ke langkah ketiga.
d. Minimum Spanning Tree (MST)
merupakan cara menemukan jalan terpendek dimana semua vertex telah terlewati sekali tanpa terjadi looping. Salah satu algoritma yang dapat digunakan untuk menyelesaikannya yaitu algoritma Prim.
Langkah-langkahnya sebagai berikut:
· Pilih sisi graf G yang berbobot paling minimum dan masukkan ke dalam T.
· Pilih sisi (u, v) yang mempunyai bobot minimum dan bersisian dengan simpul di T, tetapi tidak membentuk sirkuit di T, lalu tambahkan ke dalam T.
· Ulangi langkah kedua sebanyak n – 2 kali.
DASAR-DASAR TEORI GRAPH
Graph adalah kumpulan dari titik ( node ) dan garis dimana pasangan-pasangan titik ( node ) tersebut dihubungkan oleh segmen garis. Node ini biasa disebut simpul (verteks) dan segmen garis disebut ruas (edge).
Simpul dan ruas dalam graph dapat diperluas dengan penambahan informasi. Sebagai contoh, simpul bisa diberi nomor atau label dan ruas dapat diberi nilai juga. Perluasan dengan pemberian informasi ini sangat berguna dalam penggunaan graph untuk banyak aplikasi komputer. Contoh, graph dengan simpul yang merepresentasikan kota dan ruas merepresentasikan jarak yang ditempuh diantara kota-kota tsb. (atau harga tiket pesawat antara kota-kota tsb.) , dapat digunakan sebagai “transportation network” untuk mempelajari total jarak (atau harga) dari suatu perjalanan dengan banyak kota pemberhentian. Satu kemungkinan pertanyaan yang bisa muncul adalah “Jalur mana yang terpendek dengan satu atau lebih tempat pemberhentian, yang menghubungkan kota tertentu menuju kota tertentu lainnya dalam transportation network tersebut ?”.
Dalam kehidupan sehari-hari maupun dalam bidang akademis banyak persoalan yang dimodelkan dengan graph. Graph dipakai untuk membantu pemecahan masalah. Dari model graph yang dibuat, suatu masalah dapat dipahami menjadi lebih mudah. Untuk kemudian diturunkan metode pemecahannya.
1.1. Kelahiran Teori Graph
Gbr1. Jembatan Konigsberg
Menurut catatan sejarah, masalah jembatan Konigsberg adalah masalah yang pertama kali menggunakan graph (th. 1736). Masalah Jembatan Konigsberg adalah : “ apakah mungkin melalui tujuh buah jembatan masing-masing tepat satu kali. Dan kembali lagi ke tempat semula ?” . Tak seorangpun yang dapat memecahkan masalah ini. Barulah Euler yang pertama kali menemukan jawabannya. Ia memodelkan masalah dengan memodelkannya ke dalam graph. Daratan (titik-titik yang dihubungkan oleh jembatan) dinyatakannya sebagai simpul (vertex) dan jembatan sebagai sisi. Graph dibuat oleh Euler diperlihatkan pada gambar dibawah atas.
Jawabannya adalah : Orang tidak mungkin berjalan melalui ketujuh jembatan masing-masing satu kali dan kembali ke tempat asal keberangkatan. Singkatnya, tidak terdapat siklus Euler pada Graph tersebut.
Graph yang memenuhi kondisi diatas tersebut kemudian dikenal dengan nama Graph Euler dan perjalanannya disebut perjalanan euler.
Perjalanan Euler adalah :
Perjalanan dari suatu simpul kembali ke simpul tersebut dengan melalui setiap ruas tepat satu kali.
Perjalanan Euler akan terjadi, jika :
– Graf terhubung.
– Banyaknya ruas yang datang pada setiap simpul adalah genap
1.2. Graph secara Formal
Definisi Graf Graf G (V, E), adalah koleksi atau pasangan dua himpunan
(1) Himpunan V yang elemennya disebut simpul atau titik, atau vertex, atau point, atau node.
(2) Himpunan E yang merupakan pasangan tak terurut dari simpul, disebut ruas atau rusuk, atau sisi, atau edge, atau line.
Banyaknya simpul (anggota V) disebut order Graph G, sedangkan banyaknya ruas (anggota E) disebut ukuran (size) Graph G
e4
e3 1 e1 2 e2 3 e5 4 9
e10 e11 e12 e13
e6 e7 e8 e9 8
e14
5 6 7 e16
e15 10
Gbr 2. Graph G
Pada Gbr 2, G (V,E) adalah graph dengan
V = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
E = {e1, e2, e3, e4, e5, e6, e7, e8, e9, e10, e11, e12, e13, e14, e15, e16 }
Ruas
e1 = (1,2)
e2 = (2,3)
e3 = (1,1)
e4 = (2,4)
e5 = (3,4)
e6 = (1,5)
e7 = (1,6)
e8 = (2,6)
e9 = (2,7)
e10 = (3,8)
e11 = (4,8)
e12 = (4,7)
e13 = (4,7)
e14 = (7,8)
e15 = (5,6)
e16 = (7,10)
Pada Graph G (gbr.2) , Order = 10 dan Ukuran = 16
Pada Graph G (gbr.2), ruas e12 = (4,7) dan ruas e13 = (4,7) dinamakan ruas berganda atau ruas sejajar (multiple edges atau paralel edges), karena kedua sisi ini menghubungi dua buah simpul yang sama, yaitu simpul 4 dan simpul 7.
Pada Graph G (gbr.2), ruas e3 = (1,1) dinamakan gelung atau self-loop karena ia berawal dan berakhir pada simpul yang sama.
Derajat (Degree) suatu simpul d(v) adalah banyaknya ruas yang menghubungi simpul tersebut.
Sedangkan Derajat Graph G adalah jumlah derajat semua simpul pada Graph G.
Pada Gbr 2, derajat simpul
d(1) = 5
d(2) = 5
d(3) = 3
d(4) = 5
d(5) = 2
d(6) = 3
d(7) = 5
d(8) = 3
d(9) = 0
d(10) = 1 +
= 30
Maka derajat Graph G adalah 32 dan jumlah derajat semua simpul Graph (derajat Graph) = dua kali banyaknya ruas Graph (size/ukuran Graph).
Simpul 9 dikatakan simpul terpencil / simpul terisolasi, karena d(9) = 0 dan simpul 10 dikatakan simpul bergantung / simpul akhir karena d(10) = 1
1.3. Jenis Graph
Berdasarkan ada tidaknya gelang atau sisi ganda pada suatu graph, maka graph digolongkan menjadi dua jenis:
1. Graph sederhana (simple graph).
Graph yang tidak mengandung gelung maupun sisi-ganda dinamakan graph sederhana.
2. Graph tak-sederhana (unsimple-graph/multigraph).
Graph yang mengandung ruas ganda atau gelung dinamakan graph tak-sederhana (unsimple graph atau multigrapf).
Berdasarkan jumlah simpul pada suatu graph, maka secara umum graph dapat digolongkan menjadi dua jenis:
1. Graph berhingga (limited graph)
Graph berhingga adalah graph yang jumlah simpulnya, n, berhingga.
2. Graph tak-berhingga (unlimited graph)
Graph yang jumlah simpulnya, n, tidak berhingga banyaknya disebut graph tak-berhingga.
Berdasarkan orientasi arah pada sisi, maka secara umum graph dibedakan atas 2 jenis:
1. Graph tak-berarah (undirected graph)
Graph yang sisinya tidak mempunyai orientasi arah disebut graph tak-berarah.
2. Graph berarah (directed graph atau digraph)
Graph yang setiap sisinya diberikan orientasi arah disebut sebagai graph berarah.
e4
e3 1 e1 2 e2 3 e5 4
e10 e11
e6 e7 e8 e9
5 6
e15
Gbr 3 graph berarah
1.4. Subgraph
Misalkan G = (V, E) adalah sebuah graph. G1 = (V1, E1), jika V1 ⊆ V dan E1 ⊆ E. maka G1adalah subgraph (subgraph) dari G .
G = (V, E)
Dengan V = { A, B, C, D }
E = { e1, e2, e3, e4, e5 }
Dan
G1 = (V1, E1)
Dengan V1 = { A, B, D } ⊆ V
E1 = { e1, e5 } ⊆ E
| D |
| C |
| B |
| A |
| e5 |
| e1 |
| e3 |
| e25 |
| e4 |
| G |
| B |
| AD |
| D |
| e1 |
| e5 |
| G1 |
| D |
| C |
| B |
| e3 |
| e25 |
| e4 |
| G2 |
Komplemen dari subgraph G1 terhadap graph G adalah graph G2 = (V2, E2) sedemikian sehingga E2 = E – E1 dan V2 adalah himpunan simpul yang anggota-anggota E2 bersisian dengannya.
G = (V, E)
Dengan V = { A, B, C, D }
E = { e1, e2, e3, e4, e5 }
G1 = (V1, E1) subgraph dari G
Dengan V1 = { A, B, D } ⊆ V
E1 = { e1, e5 } ⊆ E
G2 = (V1, E1) subgraph dari G
Dengan V2 = { B, C, D } ⊆ V
E2 = { e2, e3, e4 } ⊆ E
Dan terlihat E2 = E – E1
Subgraph yang Direntang (Spanning Subgraph) Apabila E‘ mengandung semua ruas di E yang kedua ujungnya di V‘ , maka G‘ adalah Spanning Subgraph dari G yang dibentuk oleh V‘ .
G2 = (V1, E1) Spanning subgraph dari G
Dengan V2 = { B, C, D } ⊆ V
E2 = { e2, e3, e4 } ⊆ E
Anggota E2 adalah semua ruas dari G yang menghubungkan simpul di V2.
1.5. Keterhubungan Graph
| D |
| C |
| B |
| A |
| e5 |
| e1 |
| e3 |
| e25 |
| e4 |
| G |
Dua buah simpul dikatakan bertetangga (Adjacent) bila keduanya terhubung langsung oleh sebuah ruas.
Pada graph G disamping,
simpul A bertetangga dengan simpul B dan D,
simpul A tidak bertetangga dengan simpul C
Bersisian (Incidency)
Untuk sembarang ruas e = (vj, vk) dikatakan :
e bersisian dengan simpul vj , atau e bersisian dengan simpul vk
Pada graph G
ruas e5 bersisian dengan simpul A dan simpul D, tetapi
ruas e5 tidak bersisian dengan simpul B
Simpul terpencil (Isolated Vertex) ialah simpul yang tidak mempunyai sisi yang bersisian dengannya atau simpul bererajat 0 (nol).
| D |
Graf Kosong (null graf atau empty graf) adalah graf yang himpunan sisinya merupakan himpunan kosong (Nn).
| A |
| B |
| C |
Graph N4
1.6. Operasi Graph
G1 = (E1,V1) , G2 = (E2,V2)
1. Gabungan G1 ∪ G2 adalah graf dgn himpunan ruasnya E1 ∪ E2.
2. Irisan G1 ∩ G2 adalah graf dgn himpunan ruasnya E1 ∩ E2.
3. Selisih G1 – G2 adalah graf dgn himpunan ruasnya E1 – E2.
4. Selisih G2 – G1 adalah graf dgn himpunan ruasnya E2 – E1.
5. Penjumlahan ring G1 ⊕ G2 adalah graf dgn himpunan ruasnya (E1 ∪ E2) – (E1 ∩ E2) atau (E1 – E2) ∪ (E2 – E1).
| D |
| C |
| B |
| A |
| e5 |
| e1 |
| e3 |
| e25 |
| e4 |
| G1 |
| D |
| C |
| G2 – G1 |
| e6 |
| e8 |
| e7 |
| D |
| C |
| A |
| e5 |
| e4 |
| G2 |
| e6 |
| e8 |
| e7 |
| D |
| C |
| A |
| e5 |
| e4 |
| G1 G2 |
| D |
| C |
| B |
| A |
| e1 |
| e3 |
| e25 |
| G1 – G2 |
| D |
| C |
| B |
| A |
| e5 |
| e1 |
| e3 |
| e25 |
| e4 |
| G1 G2 |
| e6 |
| e8 |
| e7 |
| D |
| C |
| B |
| A |
| e1 |
| e3 |
| e25 |
| e6 |
| e8 |
| e7 |
| G2 |
| G1 |
Graph K dan L merupakan dekomposisi Suatu graf G, bila K ∪ L = G dan K ∩ L = ∅
Contoh :
Penghapusan ( deletion ) dapat dilakukan pada simpul ataupun ruas.
1) Penghapusan Simpul .
Notasinya : G – {V}
Contoh :
2) Penghapusan Ruas .
Notasinya : G – {e}
Pemendekan/Shorting adalah menghapus simpul yang dihubungkan oleh 2 ruas (simpul berderajat 2), lalu menghubungkan titik-titik ujung yang lain dari kedua ruas tersebut.
Contoh :
1.7. Keterhubungan
Perjalanan atau walk pada suatu Graf G adalah barisan simpul dan ruas berganti-ganti
v1, e1, v2, e2, …,en-1,
dengan vn simpul
ei ruas menghubungkan vi dan vi+1
dapat hanya ditulis barisan ruas atau barisan simpul saja.
e1, e2, …,en-1 atau v1, v2, …, vn-1, vn
Dalam hal ini, v1 disebut simpul awal, dan vn disebut simpul akhir.
Perjalanan disebut perjalanan tertutup bila v1 = vn, sedangkan Perjalanan disebut perjalanan tebuka yang menghubungkan v1 dan vn. Panjang Perjalanan adalah banyaknya ruas dalam barisan tersebut
Lintasan (Trail) Lintasan adalah Walk dengan semua ruas dalam barisan adalah berbeda.
Jalur adalah Walk yang semua simpul dalam barisan adalah berbeda.
Lintasan yang berawal dan berakhir pada simpul yang sama disebut sirkuit atau siklus. Panjang sirkuit adalah jumlah ruas dalam sirkuit tersebut.
Graf yang tidak mengandung sirkuit disebut acyclic.
Contoh Pohon :
Suatu graf G disebut terhubung jika untuk setiap simpul dari graf terdapat jalur yang menghubungkan kedua simpul tersebut.
Subgraf terhubung suatu graf disebut komponen dari G bila subgraf tersebut tidak terkandung dalam subgraf terhubung lain yang lebih besar.
Contoh :
Rank (G) = n – K
Nullity (G) = e – (n – k)
Dimana : n : Order graf G
e : Size graf G
K : banyaknya komponen graf G
Jarak antara 2 simpul dalam graf G adalah panjang jalur terpendek antara ke 2 simpul tersebut.
Diameter suatu graf terhubung G adalah maksimum jarak antara simpul G.
Jarak maksimum dalam graf G adalah 3 (yaitu antara A – G atau B – G ataupun C – G), jadi diameter = 3
Himpunan-Potong ( Cut-set ) dari graf terhubung G adalah himpunan ruas yang bila dibuang dari G, menyebabkan G tidak terhubung. Jadi Himpunan-Potong selalu menghasilkan dua buah komponen.
| D |
| C |
| B |
| A |
| e3 |
| e1 |
| e25 |
| e4 |
| G |
| E |
| e5 |
Himpunan {e1 , e4} adalah cut-set, juga {e2,e4}, tetapi {e3 , e5} bukan, karena {e5} adalah cut-set
1.8. Penyajian Graph
Terdapat 2 cara standard untuk menyatakan graph yaitu :
- Link list
- Matriks
Matriks-matriks yang dapat menyajikan model graf tersebut antara lain :
a) Matriks Ruas
Matriks ukuran (2 X M) atau (M X 2) yang menyatakan ruas dari Graf. Matriks ini tidak dapat mendeteksi adanya simpul terpencil, kecuali jumlah simpul yang terdapat dalam Graf disebutkan.
b) Matriks Adjacency
Notasi
Matriks adjacency merupakan matriks simetri. Elemen yang tidak bernilai nol pada diagonal utama menyatakan suatu loop. Simpul terpencil dapat dideteksi bila ada baris yang semua elemennya bernilai nol.
c) Matriks Insidensi
Notasi :
Jumlah elemen tidak nol pada suatu baris menunjukkan derajat dari simpul.
Setiap kolom mempunyai tepat dua elemen yang tidak nol. Suatu kolom yang hanya mempunyai satu elemen tidak nol menunjukkan suatu loop.
c) Matriks Connection
Notasi :
Graf terhubung jika dan hanya jika matriks tidak mengandung elemen nol. Tidak dapat mendeteksi adanya ruas sejajar dan loop.
| 4 |
| 3 |
| 2 |
| 1 |
| e5 |
| e1 |
| e3 |
| e25 |
| e4 |
| 5 |
| e71 |
| e65 |
Contoh representasi Graph :
Adjacency List
| 2 |
| 4 |
| 1 |
| 1 |
| 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 4 |
| 1 |
| 4 |
| 2 |
| 5 |
| 3 |
| 3 |
| 4 |
| 5 |




































0 komentar