TI_POLITALA_MATDIS_1A
Nama : Nordian
Kelas : 1A
Prodi : Tekinik Informatika
- RELASI
Relasi dapat mengacu kepada beberapa konsep:
Pada relasi, tidak ada aturan khusus untuk memasangkan setiap anggota himpunan daerah asal ke daerah kawan. Aturan hanya terikat atas pernyataan relasi tersebut. Setiap anggota himpunan daerah asal boleh mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan. Sedangkan pada fungsi, setiap anggota himpunan daerah asal dipasangkan dengan aturan khusus. Aturan tersebut mengharuskan setiap anggota himpunan daerah asal mempunyai pasangan dan hanya tepat satu dipasangkan dengan daerah kawannya.
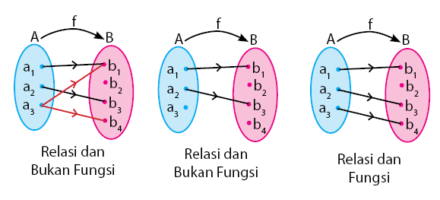
Kesimpulannya, setiap relasi belum tentu fungsi, namun setiap fungsi pasti merupakan relasi. Penjelasan mengenai relasi dan fungsi dapat dilihat pada gambar di bawah.
Selanjutnya, mari simak pembahasan lebih lanjut mengenai relasi dan fungsi pada pembahasan di bawah.
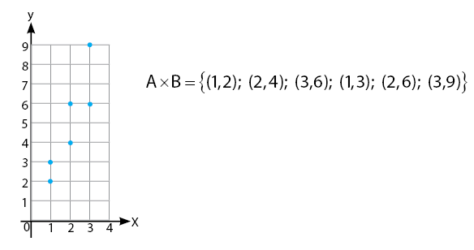
Seperti yang telah dijelaskan secara singkat di atas, relasi dapat diartikan sebagai hubungan. Misalkan sebuah relasi menyatakan hubungan perkalian. Hasil relasi tersebut dapat dinyatakan dalam himpunan pasangan terurut x dan y dan dapat juga digambar pada bidang kartesius.
Cara menyatakan hasil relasi perkalian antara himpunan A dan B dapat dilihat pada contoh permasalahan di bawah.
![Rendered by QuickLaTeX.com \[ A \; = \; \left \{ 1, \; 2, \; 3, \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d1fee107072593e46e96febee4dec418_l3.png)
![Rendered by QuickLaTeX.com \[ B \; = \; \left \{ 2, 3 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-daeb4c427f2ec88d2832af6982ed15e9_l3.png)
Fungsi atau yang sering disebut juga dengan pemetaan masih termasuk dalam relasi. Suatu relasi disebut fungsi jika semua anggota himpunan daerah asal dipasangkan tepat satu ke daerah kawannya.
Simbol fungsi yang memetakan himpunan A ke B adalah
![Rendered by QuickLaTeX.com \[ f: \; A \rightarrow B\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-6fcd2503c617afc66fb662d8ac5083a0_l3.png) Contoh pemasalahan pada fungsi:
Contoh pemasalahan pada fungsi:
Diketahui himpunan A dan B diberikan seperti di bawah.
![Rendered by QuickLaTeX.com \[ A = \left \{ 0, 1, 2, 3, 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-643bf49e5f45e692e5a4ffca0538aaeb_l3.png)
![Rendered by QuickLaTeX.com \[ B = \left \{ 0, 1, 2, ..., 10 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-440212b7cc191c741c4a0aba87d632a9_l3.png) Didefinisikan fungsi
Didefinisikan fungsi  dengan f(x) = x + 5.
dengan f(x) = x + 5.
Tentukan hasil pemetaan dari oleh fungsi
oleh fungsi 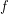 ,
,  ,
, 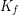 , dan
, dan 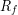 !
!
Pembahasan:
Peta dari oleh fungsi f yaitu y = f(x):
oleh fungsi f yaitu y = f(x):
![Rendered by QuickLaTeX.com \[ f(0) = 0 + 5 = 5 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c4ebb9c99c38503f006f99eb66e3b0db_l3.png)
![Rendered by QuickLaTeX.com \[ f(1) = 1 + 5 = 6 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d2118a577e3819445aa95e455f670d67_l3.png)
![Rendered by QuickLaTeX.com \[ f(2) = 2 + 5 = 7 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-03b90256b4833280c8bba9ebac02eafe_l3.png)
![Rendered by QuickLaTeX.com \[ f(3) = 3 + 5 = 8 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-9c26831a27c317d4dcb853763c6221b9_l3.png)
![Rendered by QuickLaTeX.com \[ f(4) = 4 + 5 = 9 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-eee345654dad9700db41710aaf317543_l3.png)
 = Daerah Asal
= Daerah Asal
![Rendered by QuickLaTeX.com \[ D_{f} = A = \left \{ 0, 1, 2, 3, 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-0e91b7c13ff17e363486f70d260275d6_l3.png)
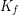 = Daerah Kawan
= Daerah Kawan
![Rendered by QuickLaTeX.com \[ K_{f} = B = \left \{ 0, 1, 2, ..., 10 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ed9c47be5a6fc3133226b166bf608a00_l3.png)
Daerah Hasil =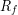
![Rendered by QuickLaTeX.com \[ D_{f} = A = \left \{5, 6, 7, 8, 9 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-31e10c571e8cd9ebd151c45afe542a75_l3.png)
- Relasi biner, konsep matematika tentang hubungan antara dua elemen himpunan
- Relasi (filsafat), konsep dalam filsafat
Pada relasi, tidak ada aturan khusus untuk memasangkan setiap anggota himpunan daerah asal ke daerah kawan. Aturan hanya terikat atas pernyataan relasi tersebut. Setiap anggota himpunan daerah asal boleh mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan. Sedangkan pada fungsi, setiap anggota himpunan daerah asal dipasangkan dengan aturan khusus. Aturan tersebut mengharuskan setiap anggota himpunan daerah asal mempunyai pasangan dan hanya tepat satu dipasangkan dengan daerah kawannya.

Kesimpulannya, setiap relasi belum tentu fungsi, namun setiap fungsi pasti merupakan relasi. Penjelasan mengenai relasi dan fungsi dapat dilihat pada gambar di bawah.
Selanjutnya, mari simak pembahasan lebih lanjut mengenai relasi dan fungsi pada pembahasan di bawah.
Daerah Asal, Kawan, dan Hasil
Dalam pembahasan relasi dan fungsi, himpunan yang terlibat digolongkan ke dalam tiga jenis daerah. Ketiga daerah tersebut adalah daerah asal (domain), daerah kawan (kodomain), dan daerah hasil (range). Secara umum, himpunan ketiga daerah tersebut dapat dilihat pada gambar di bawah.Seperti yang telah dijelaskan secara singkat di atas, relasi dapat diartikan sebagai hubungan. Misalkan sebuah relasi menyatakan hubungan perkalian. Hasil relasi tersebut dapat dinyatakan dalam himpunan pasangan terurut x dan y dan dapat juga digambar pada bidang kartesius.
Cara menyatakan hasil relasi perkalian antara himpunan A dan B dapat dilihat pada contoh permasalahan di bawah.

Fungsi atau yang sering disebut juga dengan pemetaan masih termasuk dalam relasi. Suatu relasi disebut fungsi jika semua anggota himpunan daerah asal dipasangkan tepat satu ke daerah kawannya.
Simbol fungsi yang memetakan himpunan A ke B adalah
Diketahui himpunan A dan B diberikan seperti di bawah.
Tentukan hasil pemetaan dari
Pembahasan:
Peta dari
Daerah Hasil =
Sifat-sifat Fungsi
Fungsi dikelompokkan menjadi 3 (tiga) jenis yaitu fungsi Injektif, Surjektif, dan Bijektif. Pengelompokkan tersebut didasarkan pada sifatnya. Perbedaan ketiga jenis tersebut dapat disimak pada penjelasan di bawah.- Fungsi Injektif/Fungsi Into (Fungsi Satu-satu)Fungsi pertama yang akan dibahas adalah fungsi injektif atau sering disebut dengan fungsi into atau fungsi satu-satu. Fungsi
 dikatakan fungsi injektif jika dan hanya jika anggota kodomain hanya dipasangkan satu kali dengan anggota domain.
dikatakan fungsi injektif jika dan hanya jika anggota kodomain hanya dipasangkan satu kali dengan anggota domain.
Pada fungsi injektif, anggota himpunan daerah kodomain boleh tidak memiliki pasangan, namun semua anggota kodomain yang terpsangkan hanya ada satu, tidak boleh ada yang lebih dari satu.
Perhatikan gambar di bawah untuk melihat lebih detail mengenai perbedaannya.

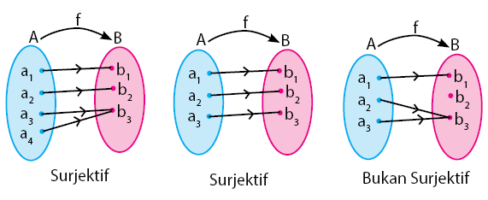
- Fungsi Surjektif (Fungsi Onto)Fungsi
Surjekti atau onto memiliki ciri yaitu anggota kodomainnya boleh
memiliki pasangan lebih dari satu, namun tidak boleh ada anggota
kodomain yang tidak dipasangkan. Fungsi surjektif biasanya dipenuhi
apabila jumlah anggota kodomain sama atau lebih banyak dari anggota
domain.
Perhatikan gambar di bawah untuk menambah pemahan sobat idschool tentang sifat fungsi surjektif.
- Fungsi Bijektif (Korespondensi Satu-satu)Fungsi
Bijektif merupakan gabungan dari fungsi injektif dan surjektif. Pada
fungsi bijektif, semua anggota domain dan kodomain terpasangkan tepat
satu. Kebalikan fungsi dari fungsi injektif dan surjektif belum pasti
fungsi/pemetaan, namun kebalikan fungsi dari fungsi bijektif juga
merupakan fungsi/pemetaan. Perhatikan gambar di bawah.
Menyatakan hubungan antara suatu anggota himpunan dengan anggota himpunan lainnya. Himpunan A dan himpunan B dikatakan memiliki relasi jika ada anggota himpunan yang saling berpasangan. Relasi antara dua himpunan dapat dinyatakan dengan tiga cara yaitu dengan diagram panah, himpunan pasangan berurutan, dan diagram Cartesius.1. Diagram PanahDiagram panah merupakan cara yang paling mudah untuk menyatakan suatu relasi. Diagram ini membentuk pola dari suatu relasi ke dalam bentuk gambar arah panah yang menyatakan hubungan antara anggota himpunan A dengan anggota himpunan B.Misalnya, ada 4 orang anak yaitu Ali, Siti, Amir dan Rizki. Mereka diminta untuk menyebutkan warna favorit mereka. Ali menyukai warna merah, Siti menyukai warna ungu, Amir menyukai warna hitam, dan Rizki menyukai warna merah. Dari hasil uraian tersebut, terdapat dua buah himpunan. Himpunan pertama adalah himpunan anak, kita sebut himpunan A dan himpunan yang kedua adalah himpunan warna, kita sebut himpunan B. Hubungan antara himpunan A dan himpunan B dapat di ilustrasikan dengan diagram panah seperti berikut:
Jadi, dapat disimpulkan bahwa diagram panah di atas merupakan relasi antara anak dengan warna yang mereka sukai. Relasi antara kedua himpunan tersebut dapat dinyatakan dengan panah-panah yang memasangkan anggota himpunan A dengan anggota himpunan B.2. Himpunan Pasangan BerurutanSelain dengan diagram panah, suatu relasi juga dapat dinyatakan dengan menggunakan himpunan pasangan berurutan. Caranya dengan memasangkan himpunan A dengan himpunan B secara berurutan. Kita dapat mengambil contoh dari contoh diagram panah tadi.Ali menyukai warna merahSiti menyukai warna unguAmir menyukai warna hitamRizki menyukai warna merahDari uraian di atas kita dapat menyatakan relasinya dengan himpunan pasangan berurutan seperti berikut:(Ali, merah), (Siti, ungu), (Amir, hitam), (Rizki, merah).Jadi, relasi antara himpunan A dengan himpunan B dinyatakan sebagai himpunan pasangan berurutan (x,y) dengan x ∈ A dan y ∈ B.3. Diagram CartesiusMenyatakan relasi antara dua himpunan dari pasangan berurutan yang kemudian dituliskan dalam bentuk dot (titik-titik). Contoh dari relasi antara anak dengan warna kesukaannya yaitu himpunan A = {Ali, Siti, Amir, Rizki} dan himpunan B = {merah, ungu, hitam}, dapat digambarkan dalam bentuk diagram Cartesius seperti di bawah ini:
FungsiFungsi (pemetaan) merupakan relasi dari himpunan A ke himpunan B, jika setiap anggota himpunan A berpasangan tepat satu dengan anggota himpunan B. Semua anggota himpunan A atau daerah asal disebut domain, sedangkan semua anggota himpunan B atau daerah kawan disebut kodomain. Hasil dari pemetaan antara domain dan kodomain disebut range fungsi atau daerah hasil. Sama halnya dengan relasi, fungsi juga dapat dinyatakan dalam bentuk diagram panah, himpunan pasangan berurutan dan dengan diagram Cartesius.Jadi, dari diagram panah di atas dapat disimpukan:Domain adalah A = {1,2,3}Kodomain adalah B = {1,2,3,4}Range fungsi = {2,3,4}Sebuah fungsi dapat dinotasikan dengan huruf kecil sepeti f, g, h. Misal, fungsi f memetakan himpunan A ke himpunan B dinotasikan f(x) dengan aturan f : x → 3x+3. Artinya fungsi f memetakan x ke 3x+3. Jadi daerah bayangan x oleh fungsi f adalah 3x+3 sehingga dapat dinotasikan dengan f(x) = 3x+3. Dari uraian ini dapat dirumuskan:Jika fungsi f : x → ax +b dengan x anggota domain f , maka rumus fungsif adalah f(x) = ax+bDengan menghitung nilai fungsi, kita dapat mengetahui nilai fungsi yang dapat menghasilkan himpunan kawan (kodomain) dari himpunan asal (domain). Supaya lebih jelas, coba kerjakan contoh soal di bawah ini ya.- Diketahui fungsi f : x → 3x + 3 pada himpunan bilangan bulat. Tentukan:
- f(3)
- bayangan (-2) oleh f
- nilai f untuk x = -4
- nilai x untuk f(x) = 6
- nilai a jika f(a) = 12
Jawab:Fungsi f : x → 3x + 3Rumus fungsi: f(x) = 3x+3- f(3) = 3(3)+3 = 12
- bayangan (-2) oleh f sama dengan f (-2), jadi f(-2) = 3(-2)+3 = -3
- nilai f untuk x = -4 adalah f (-4) = 3(-4)+3 = -9
- nilai x untuk f(x) = 6 adalah
3x + 3 = 63x = 6-33x = 3x = 15. nilai a jika f(a) = 123a + 3 = 123a = 12 – 33a = 9a = 3
-SUMBER :
https://id.wiktionary.org/wiki/relasi
https://blog.ruangguru.com/apa-itu-relasi-dan-fungsi
http://matematikalujeng.blogspot.com/2014/04/relasi-antara-anggota-dua-himpunan.html


















0 komentar